
What all of this tells us is that for a causal signal, we have convergence whenĪlthough we will not go through the process again for anticausal signals, we could. inverse Laplace transform: representation of a real or complex function f(t) of the real variable t by the integral transformation f(t) of the real variable t by the integral transformation. On the other hand, if σ+aσ a is negative or zero, the exponential will not be to a negative power, which will prevent it from tending to zero and the system will not converge. What we find is that if \(\sigma + a\) is positive, the exponential will be to a negative power, which will cause it to go to zero as tt tends to infinity. If X() is the Laplace transform of a nonnegative function x and has the.
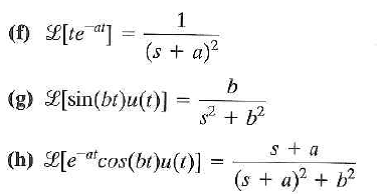
doi: 10.\) is going to determine whether this blows up or not. This is a contradiction with the definition of abscissa of convergence. For any given LTI (Section 2.1) system, some of these signals may cause the output of the system to converge, while others cause the output to diverge ('blow up'). Singhal, C, Srivastava, GS: On the growth and approximation of entire functions represented by Laplace-Stieltjes transformation. Rice University With the Laplace transform (Section 11.1), the s-plane represents a set of signals (complex exponentials (Section 1.8)). abscissa of convergence, and Example 3 has its natural boundary on. Typically the integral converges when Res. Example 1 has no singularity on its abscissa of.

We indicate a oonsequence for the Laplace transform of easures taking values in the positive cone of an ordered topological vector space. Luo, X, Liu, XZ, Kong, YY: The regular growth of Laplace-Stieltjes transforms. Then the Laplace transform of f (if it exists), is denoted by. abscissa of convergence is the same for each locally convex topology on E having the same bounded sets as. In this article, we discuss the growth of entire functions represented by LaplaceStieltjes transform converges on the whole complex plane and obtain some. Xu, HY, Xuan, ZX: The singular points of analytic functions with finite X-order defined by Laplace-Stieltjes transformations. Xu, HY, Xuan, ZX: The growth and value distribution of Laplace-Stieltjes transformations with infinite order in the right half-plane. Shang, LN, Gao, ZS: The value distribution of analytic functions defined by Laplace-Stieltjes transforms. inverse Laplace transform representation of a real or complex function f(t) of the real variable t by the integral transformation. Shang, LN, Gao, ZS: The growth of entire functions of infinite order represented by Laplace-Stieltjes transformation. Xu, HY, Yi, CF, Cao, TB: On proximate order and type functions of Laplace- Stieltjes transformations convergent in the right half-plane. other things, that >0, with 0 the convergence abscissa of the transform. Xu, HY: The logarithmic order and logarithmic type of Laplace-Stieltjes transform. Abstract The role of the Laplace transform in scientific computing has been.
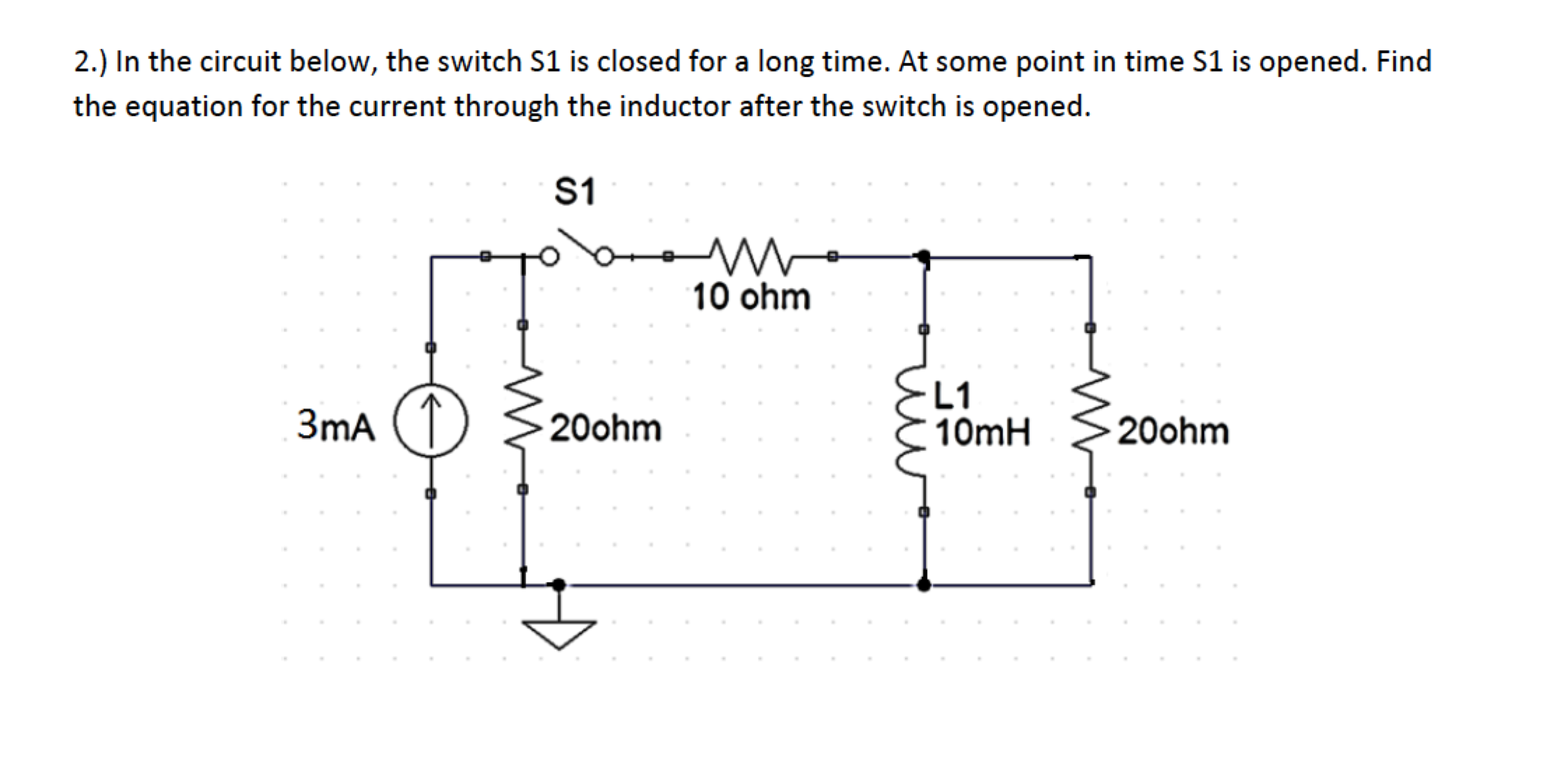
We will identify the region of convergence for the right sided causal signal. \(s=\sigma +it\) ( σ, t are real variables), \(a_\)-logarithmic type of analytic functions represented by Laplace-Stieltjes transformation. In this lesson we will understand about the concept of Region Of Convergence.


 0 kommentar(er)
0 kommentar(er)
